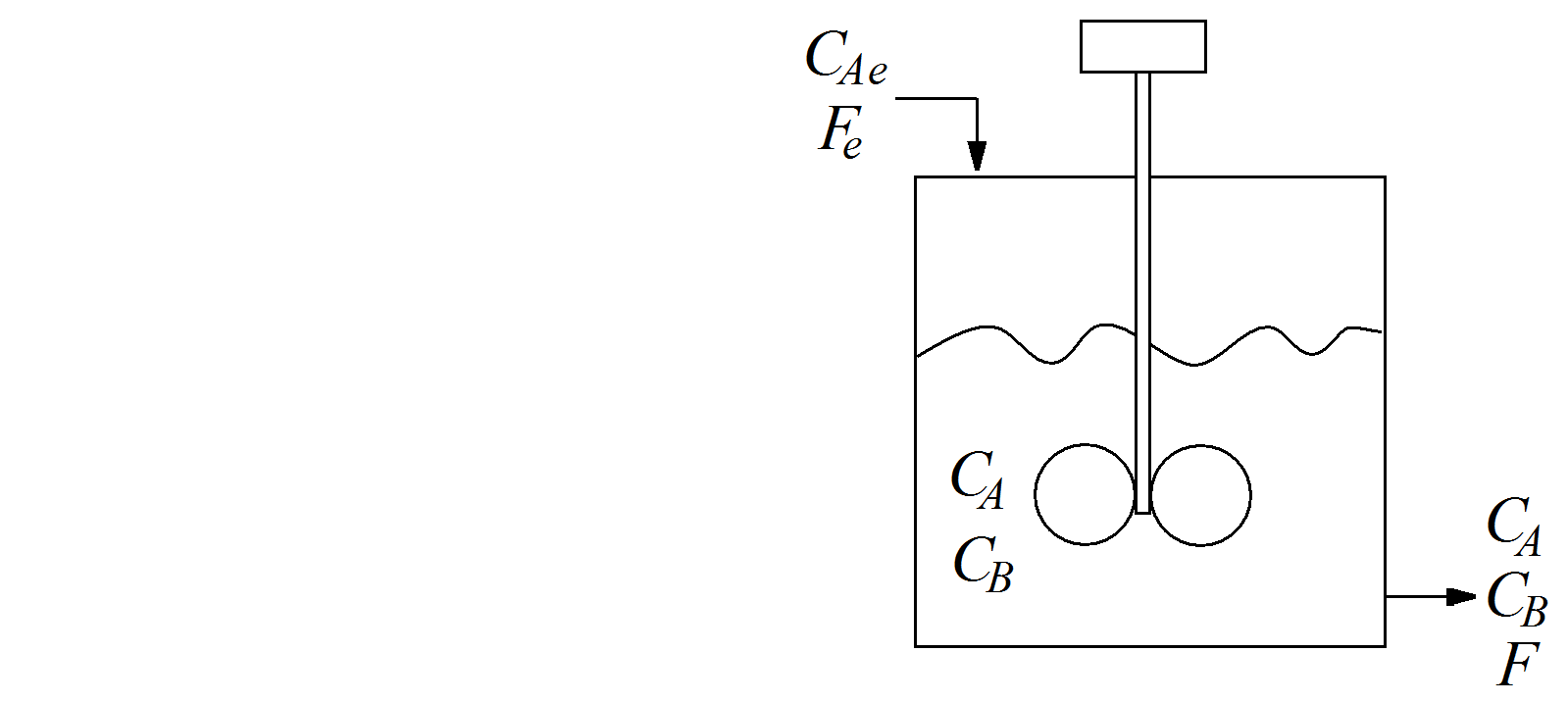
Reator CSTR Isotérmico:

Considere um reator CSTR (Continuous Stirred-Tank Reactor) em que acontece uma reação irreversível de primeira ordem (A se transformando em B) com temperatura constante, conforme a figura a seguir. O objetivo deste estudo é apresentar os perfis de concentração adimensionais, bem como analisar a influência do grupo adimensional que surge durante o processo de adimensionalização.

Hipóteses:

Para a modelagem do sistema reacional são consideradas as seguintes hipóteses (Bequette, 1998): \(i\)) propriedades físicas constantes; \(ii\)) o volume do reator é considerado constante; \(iii\)) não existe mudança de fase; \(iv\)) isotérmico; \(v\)) mistura perfeita; \(vi\)) as vazões (volumétricas) do reação são consideradas constantes; \(vii\)) reação de primeira ordem; e \(viii\)) apenas o componente A é alimentado no reator.

Modelagem Matemática:

Como o volume do reator (\(V\)) é constante, o balanço global resulta na igualdade das vazões de entrada do sistema. Já o balanço individual para cada componente (A e B) é dado pelas seguintes equações:

\[\begin{gathered} \frac{dC_A}{dt}=\frac{F}{V}(C_{Ae}-C_A)-kC_A,\;\;\;\;\;C_A(0)=C_{A0}\\ \frac{dC_B}{dt}=\frac{F}{V}(-C_B)+kC_A,\;\;\;\;\;C_B(0)=C_{B0}\end{gathered}\]

em que \(t\) é o tempo; \(C_{A}\) e \(C_{B}\) são as concentrações dos componentes A e B, respectivamente; \(F\) e \(V\) representam a vazão e o volume do sistema, respectivamente; \(C_{Ae}\) é a concentração na corrente de alimentação do componente A; \(k\) é a constante de reação e \(C_{A0}\) e \(C_{B0}\) são as concentrações iniciais dos componentes A e B dentro do reator.

O modelo acima é adimensionalizado considerando os seguintes grupos (adimensionais):

\[\begin{gathered} x_A=\frac{C_A}{C_{Ae}}\\ x_B=\frac{C_B}{C_{Ae}}\\ \tau=k t\end{gathered}\]

em que \(x_A\) e \(x_B\) são os adimensionais para a concentração de A e B, respectivamente e \(\tau\) é o adimensional para o tempo. É importante ressaltar que a adimensionalização das concentrações foi realizada em função de \(C_{Ae}\), visto que esse valor é diferente de zero (A é alimentado no reator, o que não acontece com B). Neste contexto, outros grupos poderiam ser utilizados para a adimensionalização dos modelos.

A partir da aplicação dos grupos adimensionais definidos, o sistema original pode ser escrito como:

\[\begin{gathered} \frac{dx_A}{d\tau}=\beta(1-x_A)-x_A,\;\;\;\;\;x_A(0)=\frac{C_{A0}}{C_{Ae}}\\ \frac{dx_B}{d\tau}=-\beta x_B+x_A,\;\;\;\;\;x_B(0)=\frac{C_{B0}}{C_{Ae}}\end{gathered}\] em que o parâmetro \(\beta\) é definido como \(F/(kV)\).

Neste caso, o problema original (com dimensão) tem o número de parâmetros reduzidos, isto é; de 6 (\(F\), \(V\), \(C_{Ae}\), \(k\), \(C_{A0}\) e \(C_{B0}\)) para 4 (\(\beta\), \(C_{Ae}\), \(C_{A0}\) e \(C_{B0}\)).

É importante ressaltar que as relações \(C_{A0}/C_{Ae}\) e \(C_{B0}/C_{Ae}\) também poderiam ser redefinidas, o que resultaria em um modelo com menos parâmetros. Para fins de simulação o usuário deverá entrar com as condições iniciais para as concentrações na forma adimensioanl, isto é; deverão ser informados os valores das relações \(C_{A0}/C_{Ae}\) e \(C_{B0}/C_{Ae}\), respectivamente.

Solução Analítica:

O modelo apresentado apresenta a seguinte solução analíica:

\[\begin{gathered} x_A (\tau ) = \frac{\beta }{{1 + \beta }} + \frac{{\exp \left( { - (\beta + 1)\tau } \right)\left( { - \beta + \beta x_{A\circ} + x_{A\circ} } \right)}}{{1 + \beta }}\\ x_B (\tau ) = \left( {\frac{{\exp \left( {\beta \tau } \right) - \frac{{\left( { - \beta + \beta x_{A\circ} + x_{A\circ} } \right)\beta }}{{\exp (\tau )\left( {1 + \beta } \right)}} - \frac{{ - \beta + \beta x_{A\circ} + x_{A\circ} }}{{\exp (\tau )\left( {1 + \beta } \right)}}}}{{1 + \beta }} - 1 + x_{A\circ} + x_{B\circ} } \right)\exp \left( { - \beta \tau } \right)\end{gathered}\]

em que \(x_{A\circ}\) e \(x_{B\circ}\) representam as concentrações iniciais das espécies A e B dentro do reator no instante de tempo $\tau$ igual a zero, respectivamente.

Estado Estacionário:

O estado estacionário é obtido quando as variáveis adimensionais \(x_A\) e \(x_B\) não mais dependem do tempo adimensional \(\tau\). Matematicamente, esta condição é satisfeita quanto as derivadas destas variáveis com relação ao tempo são todas iguais a zero. Neste caso, o sistema original, diferencial com relação ao tempo adimensionalizado, torna-se um puramente algébrico, dado por:

\[\begin{gathered} \beta(1-x_{Aee})-x_{Aee}=0\\ -\beta x_{Bee}+x_{Aee}=0\end{gathered}\]

em que \(x_{Aee}\) e \(x_{Bee}\) representam o estado estacionário para as concentrações dos componentes A e B, respectivamente.

O sistema acima é linear com relação as variáveis \(x_{Aee}\) e \(x_{Bee}\). Este pode ser facilmente resolvido por substituição direta, isto é:

\[\begin{gathered} x_{Aee} = \frac{\beta}{1+\beta}\\ x_{Bee} = \frac{1}{1+\beta}\end{gathered}\]

Como pode ser observado, o ponto estacionário para ambas as variáveis é função do parâmetro \(\beta\). Neste caso, pode-se avaliar a influência do mesmo no valor do estado estacionário obtido.

Solução Numérica:

O sistema que representa a variação das concentrações em função do tempo é diferencial de primeira ordem. Neste caso, o mesmo pode ser integrado numericamente usando diferentes abordagens. Nesta aplicação será empregado o Algoritmo de Runge Kutta 4a Ordem a partir das condições iniciais e número de pontos de discretização definidos pelo usuário.

Simular os Perfis de Concentração
Análise de Sensibilidade
Voltar para a página principal do LabSim-EQ