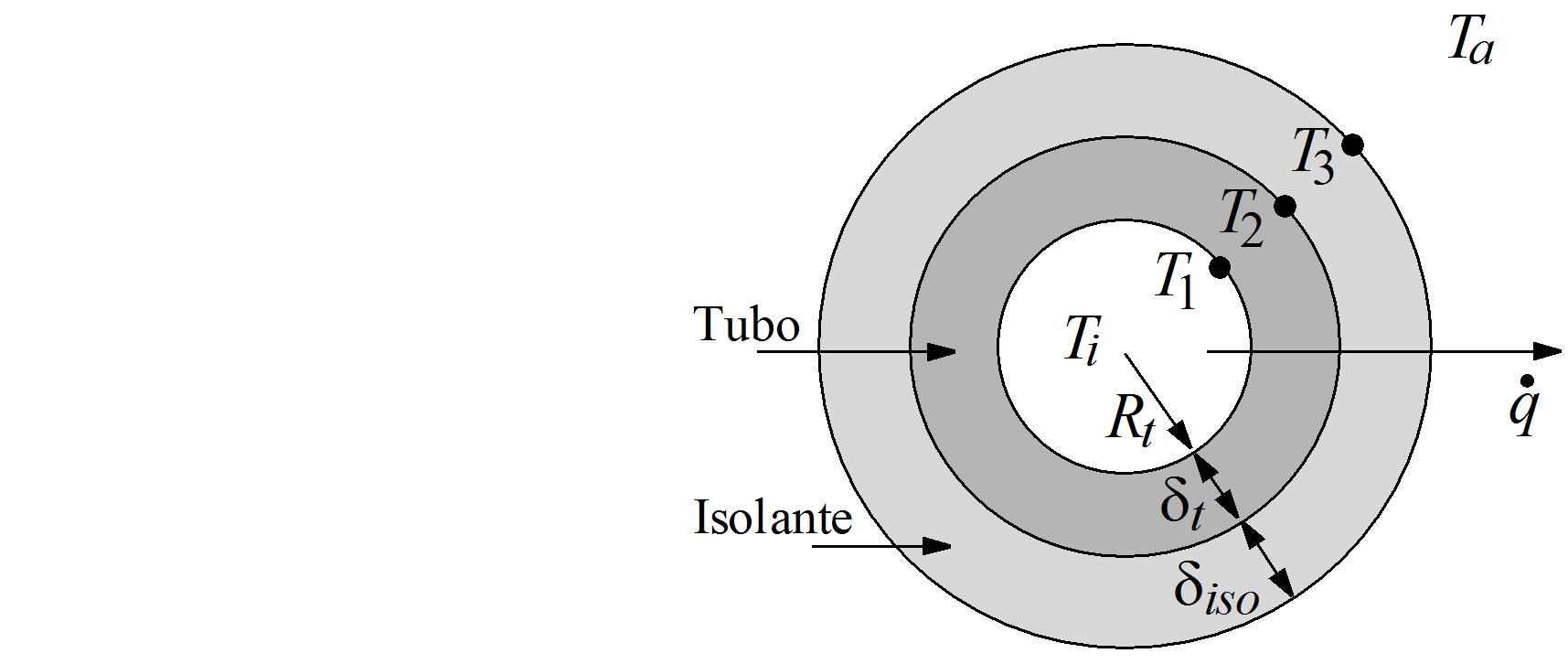
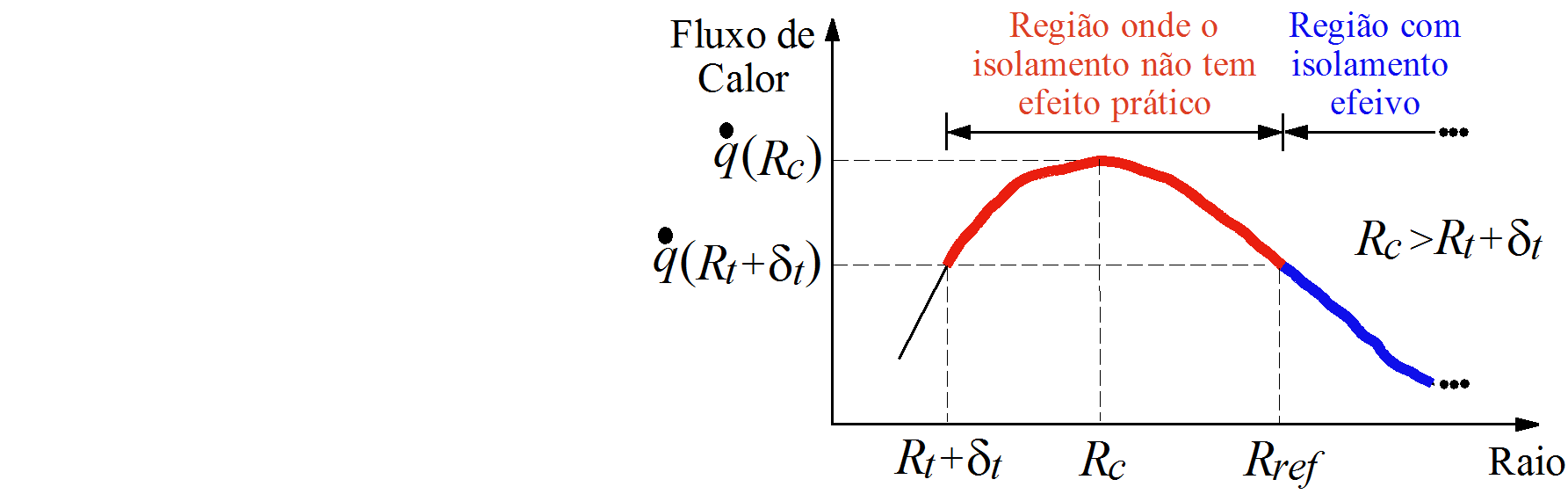
Tranferência de Calor em um Cilindro com Isolamento:

O isolamento térmico de tubulações tem como objetivo promover a redução de perdas de calor via inserção de um material isolante ao sistema original. Este tipo de abordagem apresenta inúmeras aplicações que vão deste o projeto de uma garrafa térmica ao desenvolvimento das mais sofisticadas instalações industriais. Dentre os materiais isolantes que podem ser empregados para essa finalidade destacam-se a lã de rocha, a fibra cerâmica e o poliuretano. Cabe ressaltar que a escolha do material depende de cada tipo de aplicação, dos custos e deve sempre ser avaliada previamente para cada estudo de caso.

Uma das questões mais importantes quando se faz uso de um isolante térmico é determinar a espessura ótima do mesmo, visto que neste tipo de abordagem existem efeitos concorrentes associados ao aumento dessa espessura. De forma geral em um sistema de transferência de calor com isolamento observa-se que a resistência à condução de calor aumenta com a adição de material isolante. Por outro lado, a resistência térmica à convecção de calor diminui devido ao aumento da área superficial externa. Assim, deve existir uma espessura ótima de isolante que minimize a perda de calor no sistema em análise. Diante do que foi apresentado, esta aplicação tem como objetivo avaliar o problema de traansferência de calor em um tubo cilíndrico com isolamento considerando dois aspectos, a saber, a determinação das temperaturas nas interfaces do sistema e a análise do raio crítico para fins de isolamento.

Para esta finalidade considere o transporte de vapor saturado a temperatura \(T_i\) em uma tubulação com raio interno (\(R_t\)) e espessura \(\delta_t\) que é isolada por um material com espessura \(\delta_{iso}\). Sabendo que a temperatura ambiente (\(T_a\)) é bem inferior a temperatura do vapor, o fluxo de calor \(\dot{q}\) se dará do centro da tubulação para o meio ambiente, conforme a figura a seguir.

Nesta figura, \(T_1\), \(T_2\) e \(T_3\) representam as temperaturas da parede interna da tubulação, da parede externa da tubulação (em relação a espessura \(\delta_t\)) e da parede externa do isolante (em relação a espessura \(\delta_{iso}\)).

Hipóteses e Modelagem Matemática:

Considerando que os coeficientes de transferência de calor convectivo interno (\(h_i\) - dentro do tubo) e externo (\(h_{\circ}\) - no ambiente), as condutividades térmicas do tubo (\(k_t\)) e do isolante (\(k_{iso}\)) são consideradas constantes, que não existe perda de calor, que considera-se regime estacionário, e que a temperatura do vapor é maior do que a do ambiente, este processo é modelado como segue:

Calor transferido do vapor para a tubulação

A relação a seguir diz que no ponto 1 o calor transferido do vapor por conveção deve ser igual ao calor transferido para o tubo por condução.

\[2 \pi h_i R_t \left( {T_i - T_1 } \right)=\frac{{ {2\pi k_t } \left( {T_1 - T_2 } \right)}}{\ln{((R_t+\delta_t)/R_t)}}\]

Calor transferido da tubulação para o isolante

Para o ponto 2, o calor transferido do tubo por condução deve ser igual ao calor transferido para o isolante também por condução.

\[\frac{{ {2\pi k_t } \left( {T_1 - T_2 } \right)}}{\ln{((R_t+\delta_t)/R_t)}}=\frac{{ {2\pi k_{iso} } \left( {T_2 - T_3 } \right)}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}}\]

Calor transferido do isolante para o ambiente

Finalmente no ponto 3, o calor transferido do isolante por condução deve ser igual ao calor transferido para o ambiente por convecção.

\[\frac{{\left( {2\pi k_{iso} } \right)\left( {T_2 - T_3 } \right)}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}}=2 \pi h_{\circ} (R_t+\delta_t+\delta_{iso}) \left( {T_3 - T_a } \right)\]

Solução Numérica:

No modelo apresentado deseja-se determinar os valores das temperaturas nas interfaces do sistema (\(T_1\), \(T_2\) e \(T_3\)). Neste caso, em relação a essas temperaturas tem-se um sistema linear que pode ser escrito na forma \(AT=B\), em que:

\[A=\left[ {\begin{array}{*{20}c} \frac{2k_t}{\ln{((R_t+\delta_t)/R_t)}}+2 h_i R_t & -\frac{2k_t}{\ln{((R_t+\delta_t)/R_t)}} & 0 \\ \frac{k_t}{\ln{((R_t+\delta_t)/R_t)}} & -\frac{k_t}{\ln{((R_t+\delta_t)/R_t)}}-\frac{k_{iso}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}} & \frac{k_{iso}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}} \\ 0 & \frac{2k_{iso}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}} & -\frac{2k_{iso}}{\ln{((R_t+\delta_t+\delta_{iso})/(R_t+\delta_t))}}-2h_{\circ}(R_t+\delta_t+\delta_{iso}) \\ \end{array}} \right]\]

\[T=\left[ {\begin{array}{*{20}c} {T_1 } \\ {T_2 } \\ {T_3 } \\ \end{array}} \right] \]

\[B = \left[ {\begin{array}{*{20}c} 2h_{i}R_tT_s \\ 0 \\ -2h_{\circ} (R_t+\delta_t+\delta_{iso}) T_a \\ \end{array}} \right]\]

Apesar deste sistema apresentar solução analítica, obtida pelo produto da inversa da matriz \(A\) pelo vetor \(B\), será utilizada uma abordagem iterativa, a saber, o Método de Gauss-Jacobi. Para essa finalidade, considera-se uma estimativa inicial definida pelo usuário e uma tolerância para finalizar o critério de parada adotado (somatório dos módulos dos erros absolutos de cada temperatura em duas iterações consecutivas menor que a tolerância especificada pelo usuário).

Análise do Raio Crítico:

Conforme descrito anteriormente, o fluxo de calor (\(\dot{q}\)) ou o somatório das resistências em um sistema com isolamento térmico pode ser maximizado ou minimizado. Isto irá depender da análise do raio crítico (\(R_c\)). Assim, se o sistema com isolamento for igual ao \(R_c\), o \(\dot{q}\) será maximizado, isto é; as perdas de calor serão máximas. Por outro lado, pode-se minimizar o \(\dot{q}\) se for escolhido uma espessura de isolante ideal de forma que este não coincida com o \(R_c\). A figura a seguir apresenta um tubo com isolamento térmico com a mesma estrutura descrita anteriormente, todavia com a presença do \(R_c\).

Para determinar o modelo matemático que será utilizado para a obtenção do \(R_c\), pode-se fazer uma analogia com o estudo de resistências na eletricidade, isto é; a diferença de potencial é igual ao produto da resitência pela corrente elétrica. Já no campo da transferência de calor pode-se afirmar que a diferença de temperatura será igual ao produto do fluxo de calor pelo somatório das resistências com compõem o sistema, isto é:

\[\Delta T= \dot{q} \Phi_{T}\]

em que \(\Delta_T\) é a diferença de temperatura que caracteriza o sistema (que para o sistema de interesse é \(T_i-T_a\)) e \(\Phi_T\) é o somatório das resistências, definidas como:

\[\Phi_{T}=\Phi_{i}+\Phi_{t}+\Phi_{iso}+\Phi_{\circ}\]

em que \(\Phi_{i}\) é a resistência ao transporte de calor do centro do tubo até a parede interna do mesmo, \(\Phi_{t}\) é a resistência ao transporte de calor da parede interna até a parede externa do tubo, \(\Phi_{iso}\) é a resistência ao transporte de calor da parede externa do tubo até a parede externa do isolante e \(\Phi_{\circ}\) é a resistência ao transporte de calor da parede externa do isolante até o meio ambiente. Matematicamente, estas são descritas respectivamente como:

\[\Phi_{i}=\frac{1}{2\pi h_{i} R_t L}\]

\[\Phi_{t}=\frac{\ln{((R_t+\delta_t)/R_t)}}{2\pi k_{t} L}\]

\[\Phi_{iso}=\frac{\ln{(R_c/(R_t+\delta_t))}}{2\pi k_{iso} L}\]

\[\Phi_{\circ}=\frac{1}{2\pi h_{\circ} R_c L}\]

em que \(L\) é o comprimento do cilindro.

Assim, o fluxo de calor é dado por:

\[\dot{q}=\frac{\Delta T}{\Phi_T}\]

Se plotarmos os gráficos entre \(\dot{q}\) e \(R_{c}\) e entre \(\Phi_{T}\) e \(R_{c}\) considerando todos os outros parâmetros constantes, obtêm-se um perfil bem característico para este tipo de problema:

Na figura percebe-se que existe um raio ótimo (\(R_{c}\)) para o qual o fluxo de calor é máximo. Além disso, também pode-se obserar que apenas as resistências \(\Phi_{iso}\) e \(\Phi_{\circ}\) interferem no valor da resistência total e, consequentemente, no valor do fluxo de calor (as resistências \(\Phi_{i}\) e \(\Phi_{t}\) são constantes pois não dependem do valor de \(R_{c}\)). Conforme descrito anteriormente, a resistência à condução de calor (\(\Phi_{iso}\)) aumenta com a adição de material isolante e a resitência a convecção (\(\Phi_{\circ}\)) diminui com a adição de material isolante. Como estes efeitos são concorrentes, deve existir um raio crítico ótimo que maximize a troca de calor entre o vapor e o meio ambiente. Encontrando esse valor ótimo, pode-se, a partir da análise do raio do tubo, escolher uma espessura ótima para o isolante.

O raio crítico (\(R_{c}\)) pode ser obtido a partir da maximização do fluxo de calor \(\dot{q}\) (ou da minimização da soma de todas as resistências do sistema). Devido a simplicidade do modelo apresentado, o mesmo apresenta solução analítica, obtida via maximização da seguinte equação:

\[\frac{d \dot{q}}{d R_c}=0\]

cuja solução é dada como:

\[R_c=\frac{k_{iso}{h_{\circ}}\]

De acordo com esta relação, o raio crítico para o sistema em análise é dado pelo quociente entre a condutividade térmica do isolante e o coeficiente convectivo externo (ambiente). Como deseja-se projetar um sistema com isolamento térmico, a partir da análise deste valor com relação ao raio+espessura da tubulação, poderá ser definido um valor de espessura para o isolante de forma o fluxo de calor seja reduzido. Neste caso, duas situações podem ser encontradas na prática. A primeira em que o valor de \(R_{t}+\delta_t\) é menor do que o \(R_{c}\), conforme ilustrado na figura a seguir:

Nesta figura observa-se que o fluxo de calor para \(R_{t}+\delta_t\) é igual a \(\dot{q}(R_{t}+\delta_t)\) (sem isolamento térmico) e este é menor do que o valor máximo observado, isto é; \(\dot{q}(R_{c})\). Na prática, existe um intervalo em que não se tem uma redução efetiva do fluxo de calor em relação ao valor original (\(\dot{q}(R_{t}+\delta_t)\)), isto é; entre \(R_{c}\) e o raio de referência \(R_{ref}\) tem-se inicialmente o aumento do fluxo de calor, chegando ao seu valor máximo quando o raio foi igual ao seu valor crítico, e entre \(R_{c}\) e \(R_{ref}\) tem-se a redução, mas sem ser menor do que o valor computado em \(R_{t}+\delta_t\) (\(\dot{q}(R_{t}+\delta_t)\)). Cabe ressaltar que o raio de referência (também chamado de cruzamento - do inglês crossover) é definido como o raio maior que \(R_{c}\) que apresenta o mesmo de fluxo de calor que o conjunto raio+espessura, isto é; \(\dot{q}(R_{t}+\delta_t)\). Assim, qualquer valor de raio acima de \(R_{ref}\) poderá ser empregado para minimizar o fluxo de calor com relação ao caso sem isolante térmico (\(\dot{q}(R_{t}+\delta_t)\)). A escolha desta espessura ótima após o valor de \(R_{ref}\) deverá ser realizado considerando, por exemplo, o custo do material isolante. Cabe ressaltar que, devido a natureza do modelo empregado (algébrico não-linear), o valor de \(R_{ref}\) será obtido considerando o Método de Newton.

Por outro lado, o valor do \(R_{t}+\delta_t\) pode ser maior ou igual ao \(R_{c}\), conforme apresentado na figura a seguir. Para este caso, como o valor do \(R_{t}+\delta_t\), no mínimo, coincide com o valor do \(R_{c}\), qualquer espessura de isolante que for inserida no sistema ira resultar na redução da troca de calor entre o vapor e o meio ambiente. Assim, o usuário pode escolher a espessura que mais for adequada considerando, por exemplo, o custo do material isolante. Esta situação não é a interessante do ponto de vista de projeto.

Em resumo, o raio criítico poderá ser igual, maior ou menor do que o conjunto raio+espessura da tubulação. Isto depende, como apresentado, da relação entre a condutividade térmica do isolante e o coeficiente convectivo externo (ambiente), ambos definidos pelo usuário. Finalmente, é importante ressaltar que a abordagem empregada para a determinação do raio crítico é valida para outros tipos de sistemas. Todavia, ressalta-se que, problemas com geometrias diferentes terão relações diferentes para caracterizar o raio crítico.

Determinar as Temperaturas nas Interfaces
Análise do Raio Crítico
Voltar para a página principal do LabSim-EQ